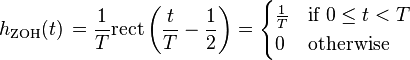Wednesday, June 3, 2015

Whoa Whoa Stop Right There.......


Dictionary.com
Jun. 03, 2015

cryptozoology		Audio Pronunciation
Share on TwitterShare on FacebookShare on Google+
\krip-toh-zoh-OL-uh-jee\
noun
1. the study of evidence tending to substantiate the existence of, or the search for, creatures whose reported existence is unproved, as the Abominable Snowman or the Loch Ness monster.
Quotes
But the tales from the cryptozoology continue, naturally, because why not let our sense of wonder be wound up by the concept of a creature affectionately known as Nessie? This cryptid is our nautical version of a Yeti or a Sasquatch that seems to lurk not only in blurry photos, but also in the darkest recesses of our dream-states.
-- Michael Cavna, "Loch Ness monster: Google Doodle plumbs the depths of our fevered fascination," Washington Post, April 21, 2015
Origin
Cryptozoology came to English in the mid-1900s from the Greek roots kryptós meaning "hidden" and zôion meaning "animal." The combining form –logy comes from the Greek word logos meaning “word” and is used in the names of sciences or bodies of knowledge.

Zoh is Only One Example of Spelling and Act Cent

Zero-order hold

From Wikipedia, the free encyclopedia
The zero-order hold (ZOH) is a mathematical model of the practical signal reconstruction done by a conventional digital-to-analog converter (DAC). That is, it describes the effect of converting a discrete-time signal to a continuous-time signal by holding each sample value for one sample interval. It has several applications in electrical communication.

Time-domain model[edit]


Figure 1. The time-shifted and time-scaled rect function used in the time-domain analysis of the ZOH.

Figure 2. Piecewise-constant signalxZOH(t).

Figure 3. A modulated Dirac combxs(t).
A zero-order hold reconstructs the following continuous-time waveform from a sample sequence x[n], assuming one sample per time interval T:
x_{\mathrm{ZOH}}(t)\,= \sum_{n=-\infty}^{\infty} x[n]\cdot \mathrm{rect} \left(\frac{t-T/2 -nT}{T} \right) \
where \mathrm{rect}() \  is the rectangular function.
The function \mathrm{rect} \left(\frac{t-T/2}{T} \right) is depicted in Figure 1, and x_{\mathrm{ZOH}}(t)\, is the piecewise-constant signal depicted in Figure 2.

Frequency-domain model[edit]

The equation above for the output of the ZOH can also be modeled as the output of a linear time-invariant filter with impulse response equal to a rect function, and with input being a sequence of dirac impulses scaled to the sample values. The filter can then be analyzed in the frequency domain, for comparison with other reconstruction methods such as the Whittaker–Shannon interpolation formula suggested by the Nyquist–Shannon sampling theorem, or such as the first-order hold or linear interpolation between sample values.
In this method, a sequence of dirac impulses, xs(t), representing the discrete samples, x[n], is low-pass filtered to recover a continuous-time signal, x(t).
Even though this is not what a DAC does in reality, the DAC output can be modeled by applying the hypothetical sequence of dirac impulses, xs(t), to a linear, time-invariant filter with such characteristics (which, for an LTI system, are fully described by the impulse response) so that each input impulse results in the correct constant pulse in the output.
Begin by defining a continuous-time signal from the sample values, as above but using delta functions instead of rect functions:
\begin{align} x_s(t) & = \sum_{n=-\infty}^{\infty} x[n]\cdot \delta\left(\frac{t - nT}{T}\right) \\ & {} = T \sum_{n=-\infty}^{\infty} x[n]\cdot \delta(t - nT). \end{align}
The scaling by T, which arises naturally by time-scaling the delta function, has the result that the mean value of xs(t) is equal to the mean value of the samples, so that the lowpass filter needed will have a DC gain of 1. Some authors use this scaling,[1] while many others omit the time-scaling and the T, resulting in a low-pass filter model with a DC gain of T, and hence dependent on the units of measurement of time.

Figure 4. Impulse response of zero-order hold hZOH(t). It is identical to the rect function of Figure 1, except now scaled to have an area of 1 so the filter will have a DC gain of 1.
The zero-order hold is the hypothetical filter or LTI system that converts the sequence of modulated Dirac impulses xs(t)to the piecewise-constant signal (shown in Figure 2):
x_{\mathrm{ZOH}}(t)\,= \sum_{n=-\infty}^{\infty} x[n]\cdot \mathrm{rect} \left(\frac{t - nT}{T}-\frac{1}{2} \right) \
resulting in an effective impulse response (shown in Figure 4) of:
h_{\mathrm{ZOH}}(t)\,= \frac{1}{T} \mathrm{rect} \left(\frac{t}{T}-\frac{1}{2} \right) = \begin{cases} \frac{1}{T} & \mbox{if } 0 \le t < T \\ 0 & \mbox{otherwise} \end{cases} \
The effective frequency response is the continuous Fourier transform of the impulse response.
H_{\mathrm{ZOH}}(f)\, = \mathcal{F} \{ h_{\mathrm{ZOH}}(t) \} \,= \frac{1 - e^{-i 2 \pi fT}}{i 2 \pi fT} = e^{-i \pi fT} \mathrm{sinc}(fT) \
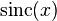where \mathrm{sinc}(x) \  is the (normalized) sinc function \frac{\sin(\pi x)}{\pi x} commonly used in digital signal processing.
The Laplace transform transfer function of the ZOH is found by substituting s = i 2 π f:
H_{\mathrm{ZOH}}(s)\, = \mathcal{L} \{ h_{\mathrm{ZOH}}(t) \} \,= \frac{1 - e^{-sT}}{s} \
The fact that practical digital-to-analog converters (DAC) do not output a sequence of dirac impulses, xs(t) (that, if ideally low-pass filtered, would result in the unique underlying bandlimited signal before sampling), but instead output a sequence of rectangular pulses, xZOH(t) (a piecewise constant function), means that there is an inherent effect of the ZOH on the effective frequency response of the DAC, resulting in a mild roll-off of gain at the higher frequencies (a 3.9224 dB loss at the Nyquist frequency, corresponding to a gain of sinc(1/2) = 2/π). This droop is a consequence of the hold property of a conventional DAC, and is not due to the sample and hold that might precede a conventionalanalog-to-digital converter (ADC).

See also[edit]

    at