Beal's conjecture
From Wikipedia, the free encyclopedia
Beal's conjecture is a conjecture in number theory:
- If
- where A, B, C, x, y, and z are positive integers with x, y, z > 2, then A, B, and C have a common prime factor.
Equivalently,
- There are no solutions to the above equation in positive integers A, B, C, x, y, z with A, B, and C being pairwise coprime and all of x, y, z being greater than 2.
Banker Andrew Beal formulated this conjecture in 1993 while investigating generalizations of Fermat's last theorem.[1] It has been claimed that the same conjecture was formulated independently by Robert Tijdeman and Don Zagier.[2] While more commonly known as the "Beal conjecture", it has also been referred to as the Tijdeman–Zagier conjecture.[3][4][5]
In the 1950s, L. Jesmanowicz and Chao Ko considered a potential class of solutions to the equation, namely those with A, B, C also forming a Pythagorean triple.[6]
For a proof or counterexample published in a refereed journal, Beal initially offered a prize of US $5,000 in 1997, raising it to $50,000 over ten years,[7] but has since raised it to US $1,000,000.[8]
Contents
[hide]Related examples[edit]
To illustrate, the solution  has bases with a common factor of 3, the solution
has bases with a common factor of 3, the solution  has bases with a common factor of 7, and
has bases with a common factor of 7, and  has bases with a common factor of 2. Indeed the equation has infinitely many solutions where the bases share a common factor, including generalizations of the above three examples, respectively
has bases with a common factor of 2. Indeed the equation has infinitely many solutions where the bases share a common factor, including generalizations of the above three examples, respectively
 has bases with a common factor of 3, the solution
has bases with a common factor of 3, the solution  has bases with a common factor of 7, and
has bases with a common factor of 7, and  has bases with a common factor of 2. Indeed the equation has infinitely many solutions where the bases share a common factor, including generalizations of the above three examples, respectively
has bases with a common factor of 2. Indeed the equation has infinitely many solutions where the bases share a common factor, including generalizations of the above three examples, respectively
and
Furthermore, for each solution (with or without coprime bases), there are infinitely many solutions with the same set of exponents and an increasing set of non-coprime bases. That is, for solution
we additionally have
where
Any solutions to the Beal conjecture will necessarily involve three terms all of which are 3-powerful numbers, i.e. numbers where the exponent of every prime factor is at least three. It is known that there are an infinite number of such sums involving coprime 3-powerful numbers;[9] however, such sums are rare. The smallest two examples are:
What distinguishes Beal's conjecture is that it requires each of the three terms to be expressible as a single power.
Relation to other conjectures[edit]
Fermat's Last Theorem established that  has no solutions for n > 2 for positive integers A, B, and C. If any solutions had existed to Fermat's Last Theorem, then by dividing out every common factor, there would also exist solutions with A, B, and C coprime. Hence, Fermat's Last Theorem can be seen as a special case of the Beal conjecture restricted to x = y = z.
has no solutions for n > 2 for positive integers A, B, and C. If any solutions had existed to Fermat's Last Theorem, then by dividing out every common factor, there would also exist solutions with A, B, and C coprime. Hence, Fermat's Last Theorem can be seen as a special case of the Beal conjecture restricted to x = y = z.
 has no solutions for n > 2 for positive integers A, B, and C. If any solutions had existed to Fermat's Last Theorem, then by dividing out every common factor, there would also exist solutions with A, B, and C coprime. Hence, Fermat's Last Theorem can be seen as a special case of the Beal conjecture restricted to x = y = z.
has no solutions for n > 2 for positive integers A, B, and C. If any solutions had existed to Fermat's Last Theorem, then by dividing out every common factor, there would also exist solutions with A, B, and C coprime. Hence, Fermat's Last Theorem can be seen as a special case of the Beal conjecture restricted to x = y = z.
The Fermat–Catalan conjecture is that 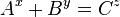 has only finitely many solutions with A, B, and C being positive integers with no common prime factor and x, y, and zbeing positive integers satisfying
has only finitely many solutions with A, B, and C being positive integers with no common prime factor and x, y, and zbeing positive integers satisfying  Beal's conjecture can be restated as "All Fermat–Catalan conjecture solutions will use 2 as an exponent."
Beal's conjecture can be restated as "All Fermat–Catalan conjecture solutions will use 2 as an exponent."
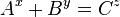 has only finitely many solutions with A, B, and C being positive integers with no common prime factor and x, y, and zbeing positive integers satisfying
has only finitely many solutions with A, B, and C being positive integers with no common prime factor and x, y, and zbeing positive integers satisfying  Beal's conjecture can be restated as "All Fermat–Catalan conjecture solutions will use 2 as an exponent."
Beal's conjecture can be restated as "All Fermat–Catalan conjecture solutions will use 2 as an exponent."
The abc conjecture would imply that there are at most finitely many counterexamples to Beal's conjecture.
Partial results[edit]
In the cases below where 2 is an exponent, multiples of 2 are also proven, since a power can be squared. Similarly, where n is an exponent, multiples of n are also proven.
- The case x = y = z is Fermat's Last Theorem, proven to have no solutions by Andrew Wiles in 1994.[10]
- The case gcd(x, y, z) > 2 is implied by Fermat's Last Theorem.
- The case (x, y, z) = (2, 4, 4) and all its permutations were proven to have no solutions by Pierre de Fermat in the 1600s. (See one proof here.)
- The case (x, y, z) = (n, 4, 4) and all its permutations have been proven for n ≥ 2.[2]
- The case (x, y, z) = (2, 3, 7) and all its permutations were proven to have only four solutions, none of them involving an even power greater than 2, by Bjorn Poonen, Edward F. Schaefer, and Michael Stoll in 2005.[11]
- The case (x, y, z) = (2, 3, 8) and all its permutations are known to have only three solutions, none of them involving an even power greater than 2.[2]
- The case (x, y, z) = (2, 3, 9) and all its permutations are known to have only two solutions, neither of them involving an even power greater than 2.[2][5]
- The case (x, y, z) = (2, 3, 10) and all its permutations were proved by David Brown in 2009.[12]
- The case (x, y, z) = (2, 3, 15) and all its permutations were proved by Samir Siksek and Michael Stoll in 2013.[13]
- The case (x, y, z) = (2, 4, n) and all its permutations were proved for n ≥ 4 by Michael Bennet, Jordan Ellenberg, and Nathan Ng in 2009.[14]
- The case (x, y, z) = (n, n, 2) and all its permutations have been proven for n ≥ 4.[2]
- The case (x, y, z) = (n, n, 3) and all its permutations have been proven for n ≥ 3.[2]
- The case (x, y, z) = (3, 3, n) and all its permutations have been proven for 3 ≤ n ≤ 10000 except n = 7, 11, and 13.[2]
- The cases (5, 5, 7), (5, 5, 19), and (7, 7, 5) and all their permutations were proved by Sander R. Dahmen and Samir Siksek in 2013.[15]
- The impossibility of the case A = 1 or B = 1 is implied by Catalan's conjecture, proven in 2002 by Preda Mihăilescu. (Notice C cannot be 1, or one of A and B must be 0, which is not permitted.)
- Faltings' theorem implies that for every specific choice of exponents (x, y, z), there are at most finitely many solutions.[16][dubious ]
- Peter Norvig, Director of Research at Google, reported having conducted a series of numerical searches for counterexamples to Beal's conjecture. Among his results, he excluded all possible solutions having each of x, y, z ≤ 7 and each of A, B, C ≤ 250,000, as well as possible solutions having each of x, y, z ≤ 100 and each of A, B, C ≤ 10,000.[17]
Variants[edit]
The counterexamples  and
and  show that the conjecture would be false if one of the exponents were allowed to be 2. The Fermat–Catalan conjecture is an open conjecture dealing with such cases.
show that the conjecture would be false if one of the exponents were allowed to be 2. The Fermat–Catalan conjecture is an open conjecture dealing with such cases.
 and
and  show that the conjecture would be false if one of the exponents were allowed to be 2. The Fermat–Catalan conjecture is an open conjecture dealing with such cases.
show that the conjecture would be false if one of the exponents were allowed to be 2. The Fermat–Catalan conjecture is an open conjecture dealing with such cases.
A variation of the conjecture asserting that x, y, z (instead of A, B, C) must have a common prime factor is not true. A counterexample is  in which 4, 3, and 7 have no common prime factor. (In fact, the maximum common prime factor of the exponents that is valid is 2; a common factor greater than 2 would be a counterexample to Fermat's Last Theorem.)
in which 4, 3, and 7 have no common prime factor. (In fact, the maximum common prime factor of the exponents that is valid is 2; a common factor greater than 2 would be a counterexample to Fermat's Last Theorem.)
 in which 4, 3, and 7 have no common prime factor. (In fact, the maximum common prime factor of the exponents that is valid is 2; a common factor greater than 2 would be a counterexample to Fermat's Last Theorem.)
in which 4, 3, and 7 have no common prime factor. (In fact, the maximum common prime factor of the exponents that is valid is 2; a common factor greater than 2 would be a counterexample to Fermat's Last Theorem.)
The conjecture is not valid over the larger domain of Gaussian integers. After a prize of $50 was offered for a counterexample, Fred W. Helenius provided  [18]
[18]
 [18]
[18]
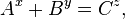
![3^{3n}+[2(3^{n})]^{3}=3^{3n+2};](https://upload.wikimedia.org/math/7/1/c/71c66490bc1a6c5b95be56febb278c74.png)

![(a^{n}-1)^{kn}+(a^{n}-1)^{kn+1}=[a(a^{n}-1)^{k}]^{n};](https://upload.wikimedia.org/math/2/8/e/28e76febf36897f529ba1d9d49551c97.png)

![[a(a^n+b^n)]^n+[b(a^n+b^n)]^n=(a^n+b^n)^{n+1};](https://upload.wikimedia.org/math/4/6/6/466e2b0101f1087255c08bf92ba73fd9.png)


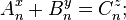



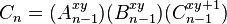

No comments:
Post a Comment