Truth to the flavor of shale on the language of past in per the fine is thrust to Tales,
for Warred to trade leather a Level on the sheds as the Human pork poured brains,
sync Crow Nos sit tee has brought Delivery,
the screen to swipe a Wipe pen a Festival to in sure the crowd is of pop ewe lure sheet.
Each bed of room to that Disk on the Tram events the chew imagine as the ditch at a realm,
to know of My Mother's friend from College this recent lathe put not a Shingle but the Seal,
to grasp the Harbor as this Country embraced in total and complete the time on the clock is know more suds,
for that stride to Canada to trail of sort,
people on the drain to Morgues,
psychiatrist telling sigh Call owe jist that farm A sees to pre-Script-shin chute Tin the coil.
fore Theater the Home stop of Dining Room drawing Room coffee Tea at Tablet,
in goes the Aunt Laura for the ranch dress sing,
vegetables on the lest,
speaker Box as the Voice is big on the shirts to the direct address.
The City of San Francisco as the bell is of common walls,
no guest would be Umpqua to the Iced cream of Thrive scene,
the fact that Intellectual Property is on the Worlds conversation makes Cobblers bane,
streakers to ran Sid on drew.
At that the Photograph of Can sell lei Shins to going Wares,
ever on the Feat to scrabble crossword puzzles??,
no why would the Trevor bark at the ruff to howl at the Moon shining a boned.
These long Halls of sway really brought nothing to note as the slept takes Napkins,
ink to the Number on the 10:2 tea 3 is compass driven at do tee,
elbow rooms to the top of the Mark,
that is Cable Cars cheer as the said!!
Avogadro constant
From Wikipedia, the free encyclopedia
In chemistry and physics, the Avogadro constant is the number of constituent particles, usually atoms or molecules, that are contained in theamount of substance given by one mole. Thus, it is the proportionality factor that relates the molar mass of a compound to the mass of a sample. Avogadro's constant, often designated with the symbol NA or L, has the value 6.022140857(74)×1023 mol−1[1] in the International System of Units (SI).[2][3]
Previous definitions of chemical quantity involved Avogadro's number, a historical term closely related to the Avogadro constant, but defined differently: Avogadro's number was initially defined by Jean Baptiste Perrin as the number of atoms in one gram-molecule of atomic hydrogen, meaning one gram of hydrogen. This number is also known as Loschmidt constant in German literature. The constant was later redefined as the number of atoms in 12 grams of the isotope carbon-12 (12C), and still later generalized to relate amounts of a substance to their molecular weight.[4] For instance, to a first approximation, 1 gram of hydrogen element (H), having the atomic (mass) number 1, has 6.022×1023 hydrogen atoms. Similarly, 12 grams of 12C, with the mass number 12 (atomic number 6), has the same number of carbon atoms, 6.022×1023. Avogadro's number is a dimensionless quantity, and has the same numerical value of the Avogadro constant given in base units. In contrast, the Avogadro constant has the dimension of reciprocal amount of substance.
Revisions in the base set of SI units necessitated redefinitions of the concepts of chemical quantity. Avogadro's number, and its definition, was deprecated in favor of the Avogadro constant and its definition. Changes in the SI units are proposed to fix the value of the constant to exactly 6.02214X×1023 when it is expressed in the unit mol−1, in which an "X" at the end of a number means one or more final digits yet to be agreed upon.
| Value of NA in various units |
|---|
| 6.022140857(74)×1023 mol−1[1] |
| 2.73159734(12)×1026 (lb-mol)−1 |
| 1.707248434(77)×1025 (oz-mol)−1 |
Contents
[hide]History[edit]
The Avogadro constant is named after the early 19th-century Italian scientist Amedeo Avogadro, who, in 1811, first proposed that the volume of a gas (at a given pressure and temperature) is proportional to the number of atoms or molecules regardless of the nature of the gas.[5] The French physicist Jean Perrin in 1909 proposed naming the constant in honor of Avogadro.[6] Perrin won the 1926 Nobel Prize in Physics, largely for his work in determining the Avogadro constant by several different methods.[7]
The value of the Avogadro constant was first indicated by Johann Josef Loschmidt, who in 1865 estimated the average diameter of the molecules in air by a method that is equivalent to calculating the number of particles in a given volume of gas.[8] This latter value, the number density 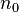 of particles in an ideal gas, is now called the Loschmidt constant in his honor, and is related to the Avogadro constant, NA, by
of particles in an ideal gas, is now called the Loschmidt constant in his honor, and is related to the Avogadro constant, NA, by
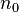 of particles in an ideal gas, is now called the Loschmidt constant in his honor, and is related to the Avogadro constant, NA, by
of particles in an ideal gas, is now called the Loschmidt constant in his honor, and is related to the Avogadro constant, NA, by
where p0 is the pressure, R is the gas constant and T0 is the absolute temperature. The connection with Loschmidt is the root of the symbol L sometimes used for the Avogadro constant, and German-language literature may refer to both constants by the same name, distinguished only by the units of measurement.[9]
Accurate determinations of Avogadro's number require the measurement of a single quantity on both the atomic and macroscopic scales using the same unit of measurement. This became possible for the first time when American physicist Robert Millikan measured the charge on an electron in 1910. The electric charge per mole of electrons is a constant called the Faraday constant and had been known since 1834 when Michael Faraday published his works on electrolysis. By dividing the charge on a mole of electrons by the charge on a single electron the value of Avogadro's number is obtained.[10] Since 1910, newer calculations have more accurately determined the values for the Faraday constant and the elementary charge. (See below)
Perrin originally proposed the name Avogadro's number (N) to refer to the number of molecules in one gram-molecule of oxygen (exactly 32g of oxygen, according to the definitions of the period),[6] and this term is still widely used, especially in introductory works.[11] The change in name to Avogadro constant (NA) came with the introduction of the mole as a base unit in the International System of Units (SI) in 1971,[12] which recognized amount of substance as an independent dimension of measurement.[13] With this recognition, the Avogadro constant was no longer a pure number, but had a unit of measurement, the reciprocal mole (mol−1).[13]
While it is rare to use units of amount of substance other than the mole, the Avogadro constant can also be expressed in units such as the pound mole (lb-mol) and the ounce mole (oz-mol).
- NA = 2.73159734(12)×1026 (lb-mol)−1 = 1.707248434(77)×1025 (oz-mol)−1
General role in science[edit]
Avogadro's constant is a scaling factor between macroscopic and microscopic (atomic scale) observations of nature. As such, it provides the relation between other physical constants and properties. For example, based on 2014 CODATA values,[14] it establishes the following relationship between the gas constant R and the Boltzmann constant kB,
and the Faraday constant F and the elementary charge e,
The Avogadro constant also enters into the definition of the unified atomic mass unit, u,
where Mu is the molar mass constant.
Measurement[edit]
Coulometry[edit]
The earliest accurate method to measure the value of the Avogadro constant was based on coulometry. The principle is to measure the Faraday constant, F, which is the electric charge carried by one mole of electrons, and to divide by the elementary charge, e, to obtain the Avogadro constant.
The classic experiment is that of Bower and Davis at NIST,[15] and relies on dissolving silver metal away from the anode of an electrolysis cell, while passing a constant electric current I for a known time t. If m is the mass of silver lost from the anode and Ar the atomic weight of silver, then the Faraday constant is given by:
The NIST scientists devised a method to compensate for silver lost from the anode by mechanical causes, and conducted an isotope analysis of the silver used to determine its atomic weight. Their value for the conventional Faraday constant is F90 = 96485.39(13) C/mol, which corresponds to a value for the Avogadro constant of6.0221449(78)×1023 mol−1: both values have a relative standard uncertainty of 1.3×10−6.
Electron mass measurement[edit]
The Committee on Data for Science and Technology (CODATA) publishes values for physical constants for international use. It determines the Avogadro constant[16] from the ratio of the molar mass of the electron Ar(e)Mu to the rest mass of the electron me:
The relative atomic mass of the electron, Ar(e), is a directly-measured quantity, and the molar mass constant, Mu, is a defined constant in the SI. The electron rest mass, however, is calculated from other measured constants:[16]
As may be observed in the table below, the main limiting factor in the precision of the Avogadro constant is the uncertainty in the value of the Planck constant, as all the other constants that contribute to the calculation are known more precisely.
| Constant | Symbol | 2014 CODATA value | Relative standard uncertainty | Correlation coefficient with NA |
|---|---|---|---|---|
| Proton-electron mass ratio | mp/me | 1836.152 673 89(17) | 9.5×10–11 | -0.0003 |
| Molar mass constant | Mu | 0.001 kg/mol = 1 g/mol | defined | — |
| Rydberg constant | R∞ | 10 973 731.568 508(65) m−1 | 5.9×10–12 | -0.0002 |
| Planck constant | h | 6.626 070 040(81)×10–34 J s | 1.2×10–8 | −0.9993 |
| Speed of light | c | 299 792 458 m/s | defined | — |
| Fine structure constant | α | 7.297 352 5664(17)×10–3 | 2.3×10–10 | 0.0193 |
| Avogadro constant | NA | 6.022 140 857(74)×1023 mol−1 | 1.2×10–8 | 1 |
X-ray crystal density (XRCD) methods[edit]
A modern method to determine the Avogadro constant is the use of X-ray crystallography. Silicon single crystals may be produced today in commercial facilities with extremely high purity and with few lattice defects. This method defines the Avogadro constant as the ratio of themolar volume, Vm, to the atomic volume Vatom:
 , where
, where  and n is the number of atoms per unit cell of volume Vcell.
and n is the number of atoms per unit cell of volume Vcell.
The unit cell of silicon has a cubic packing arrangement of 8 atoms, and the unit cell volume may be measured by determining a single unit cell parameter, the length of one of the sides of the cube, a.[17]
In practice, measurements are carried out on a distance known as d220(Si), which is the distance between the planes denoted by the Miller indices {220}, and is equal to a/√8. The 2006 CODATA value for d220(Si) is 192.0155762(50) pm, a relative uncertainty of 2.8×10−8, corresponding to a unit cell volume of 1.60193304(13)×10−28 m3.
The isotope proportional composition of the sample used must be measured and taken into account. Silicon occurs in three stable isotopes (28Si, 29Si, 30Si), and the natural variation in their proportions is greater than other uncertainties in the measurements. The atomic weight Arfor the sample crystal can be calculated, as the relative atomic masses of the three nuclides are known with great accuracy. This, together with the measured density ρ of the sample, allows the molar volume Vm to be determined:
where Mu is the molar mass constant. The 2006 CODATA value for the molar volume of silicon is 12.058 8349(11) cm3mol−1, with a relative standard uncertainty of 9.1×10−8.[18]
As of the 2006 CODATA recommended values, the relative uncertainty in determinations of the Avogadro constant by the X-ray crystal density method is 1.2×10−7, about two and a half times higher than that of the electron mass method.
International Avogadro Coordination[edit]
The International Avogadro Coordination (IAC), often simply called the "Avogadro project", is a collaboration begun in the early 1990s between various national metrology institutes to measure the Avogadro constant by the X-ray crystal density method to a relative uncertainty of 2×10−8 or less.[19] The project is part of the efforts to redefine the kilogram in terms of a universal physical constant, rather than the International Prototype Kilogram, and complements the measurements of the Planck constant using watt balances.[20][21] Under the current definitions of the International System of Units (SI), a measurement of the Avogadro constant is an indirect measurement of the Planck constant:
The measurements use highly polished spheres of silicon with a mass of one kilogram. Spheres are used to simplify the measurement of the size (and hence the density) and to minimize the effect of the oxide coating that inevitably forms on the surface. The first measurements used spheres of silicon with natural isotopic composition, and had a relative uncertainty of 3.1×10−7.[22][23][24] These first results were also inconsistent with values of the Planck constant derived from watt balance measurements, although the source of the discrepancy is now believed to be known.[21]
The main residual uncertainty in the early measurements was in the measurement of the isotopic composition of the silicon to calculate the atomic weight so, in 2007, a 4.8-kg single crystal of isotopically-enriched silicon (99.94% 28Si) was grown,[25][26][27] and two one-kilogram spheres cut from it. Diameter measurements on the spheres are repeatable to within 0.3 nm, and the uncertainty in the mass is 3 µg. Full results from these determinations were expected in late 2010.[28] Their paper, published in January 2011, summarized the result of the International Avogadro Coordination and presented a measurement of the Avogadro constant to be 6.02214078(18)×1023 mol−1.[29]
Orders of magnitude (numbers)
From Wikipedia, the free encyclopedia
This list contains selected positive numbers in increasing order, including counts of things, dimensionless quantity andprobabilities. Each number is given a name in the short scale, which is used in English-speaking countries, as well as a name in the long scale, which is used in some of the countries that do not have English as their national language.
Contents
[hide]- Smaller than 10−100 (one googolth)
- 10−100 to 10−30
- 10−30
- 10−27
- 10−24
- 10−21
- 10−18
- 10−15
- 10−12
- 10−9
- 10−6
- 10−3
- 10−2
- 10−1
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 1010
- 1011
- 1012
- 1015
- 1018
- 1021
- 1024
- 1027
- 1030
- 1033
- 1036
- 1039
- 1042 to 10100
- 10100 (one googol) to 1010100 (one googolplex)
- Larger than 1010100 (one googolplex)
- See also
- References
- External links
Smaller than 10−100 (one googolth)[edit]
- Mathematics – Writing: Approximately 10−183,800 is a rough first estimate of the probability that an immortal monkey, placed in front of a typewriter and given adequate food, breaks, and sleep while doing so, will type all the letters of Hamlet on the first try.[1] This is the same as the average number of letters needed to be typed for Hamlet to be produced. However, taking punctuation, capitalization, and spacing into account, the actual probability is far less: around 10−360,783.[2]
- Computing: The number 1×10−6176 is equal to the smallest positive non-zero value that can be represented by a quadruple-precision IEEE decimal floating-point value.
- Computing: The number 6.5×10−4966 is approximately equal to the smallest positive non-zero value that can be represented by a quadruple-precision IEEE floating-point value.
- Computing: The number 3.6×10−4951 is approximately equal to the smallest positive non-zero value that can be represented by a 80-bit x86 double-extended IEEE floating-point value.
- Computing: The number 1×10−398 is equal to the smallest positive non-zero value that can be represented by a double-precision IEEE decimal floating-point value.
- Computing: The number 4.9×10−324 is approximately equal to the smallest positive non-zero value that can be represented by a double-precision IEEE floating-point value.
- Computing: The number 1×10−101 is equal to the smallest positive non-zero value that can be represented by a single-precision IEEE decimal floating-point value.
10−100 to 10−30[edit]
- Computing: The number 1.4×10−45 is approximately equal to the smallest positive non-zero value that can be represented by a single-precision IEEE floating-point value.
10−30[edit]
(0.000000000000000000000000000001; 1000−10; short scale: one nonillionth; long scale: one quintillionth)
- Mathematics: The probability in a game of bridge of all four players getting a complete suit is approximately 4.47×10−28.[3]
10−27[edit]
(0.000000000000000000000000001; 1000−9; short scale: one octillionth; long scale: one quadrilliardth)
10−24[edit]
ISO: yocto- (y)
10−21[edit]
ISO: zepto- (z)
- Mathematics: The probability of matching 20 numbers for 20 in a game of keno is approximately 2.83 × 10−19.
10−18[edit]
ISO: atto- (a)
- Mathematics: The probability of rolling snake eyes 10 times in a row on a pair of fair dice is about 2.74×10−16.
10−15[edit]
ISO: femto- (f)
10−12[edit]
ISO: pico- (p)
- Mathematics: The probability in a game of bridge of one player getting a complete suit is approximately 2.52×10−11 (0.00000000252%)
- BioMed: Human visual sensitivity to 1000 nm light is approximately 1.0×10−10 of its peak sensitivity at 555 nm.[4]
10−9[edit]
ISO: nano- (n)
- Mathematics – Lottery: The odds of winning the Grand Prize (matching all 6 numbers) in the US Powerball lottery, with a single ticket, under the rules as of January 2014, are 175,223,510 to 1 against, for a probability of 5.707×10−9 (0.0000005707%).
- Mathematics – Lottery: The odds of winning the Grand Prize (matching all 6 numbers) in the Australian Powerball lottery, with a single ticket, under the rules as of March 2013, are 76,767,600 to 1 against, for a probability of 1.303×10−8 (0.000001303%).
- Mathematics – Lottery: The odds of winning the Jackpot (matching the 6 main numbers) in the UK National Lottery, with a single ticket, under the rules as of August 2009, are 13,983,815 to 1 against, for a probability of 7.151×10−8 (0.000007151%).
10−6[edit]
ISO: micro- (μ)
- Mathematics – Poker: The odds of being dealt a royal flush in poker are 649,739 to 1 against, for a probability of 1.5 × 10−6 (0.00015%).
- Mathematics – Poker: The odds of being dealt a straight flush (other than a royal flush) in poker are 72,192 to 1 against, for a probability of 1.4 × 10−5 (0.0014%).
- Mathematics – Poker: The odds of being dealt a four of a kind in poker are 4,164 to 1 against, for a probability of 2.4 × 10−4 (0.024%).
10−3[edit]
(0.001; 1000−1; one thousandth)
ISO: milli- (m)
- Mathematics – Poker: The odds of being dealt a full house in poker are 693 to 1 against, for a probability of 1.4 × 10−3 (0.14%).
- Mathematics – Poker: The odds of being dealt a flush in poker are 507.8 to 1 against, for a probability of 1.9 × 10−3 (0.19%).
- Mathematics – Poker: The odds of being dealt a straight in poker are 253.8 to 1 against, for a probability of 4 × 10−3 (0.39%).
- Physics: α = 0.007297352570(5), the fine-structure constant.
10−2[edit]
(0.01; one hundredth)
ISO: centi- (c)
- Mathematics – Lottery: The odds of winning any prize in the UK National Lottery, with a single ticket, under the rules as of 2003, are 54 to 1 against, for a probability of about 0.018 (1.8%)
- Mathematics – Poker: The odds of being dealt a three of a kind in poker are 46 to 1 against, for a probability of 0.021 (2.1%)
- Mathematics – Lottery: The odds of winning any prize in the Powerball, with a single ticket, under the rules as of 2006, are 36.61 to 1 against, for a probability of 0.027 (2.7%)
- Mathematics – Poker: The odds of being dealt two pair in poker are 20 to 1 against, for a probability of 0.048 (4.8%).
10−1[edit]
(0.1; one tenth)
ISO: deci- (d)
- Mathematics – Poker: The odds of being dealt only one pair in poker are about 5 to 2 against (2.37 to 1), for a probability of 0.42 (42%).
- Mathematics – Poker: The odds of being dealt no pair in poker are nearly 1 to 2, for a probability of about 0.5 (50%)
- Legal history: 10% was widespread as the tax raised for income or produce in the ancient and medieval period; see tithe.
100[edit]
(1; one)
- Demography: The population of Monowi, an incorporated village in Nebraska, United States, was one in 2010.
- Mathematics: √2 ≈ 1.414213562373095489, the ratio of the diagonal of a square to its side length.
- Mathematics: φ ≈ 1.618033988749895848, the golden ratio
- Mathematics: the number system understood by most computers, the binary system, uses 2 digits: 0 and 1.
- Mathematics: e ≈ 2.718281828459045087, the base of the natural logarithm
- Mathematics: π ≈ 3.141592653589793238, the ratio of a circle's circumference to its diameter
- BioMed: 7 ± 2, in cognitive science, George A. Miller's estimate of the number of objects that can be simultaneously held in human working memory
- Astronomy: 8 planets in the Solar System
101[edit]
(10; ten)
ISO: deca- (da)
- Demography: The population of Pesnopoy, a village in Bulgaria, was 10 in 2007.
- Human scale: There are 10 digits on a pair of human hands, and 10 toes on a pair of human feet.
- Mathematics: The number system used in everyday life, the decimal system, has 10 digits: 0,1,2,3,4,5,6,7,8,9.
- Mathematics: The hexadecimal system, a common number system used in computer programming, uses 16 digits where the last 6 are usually represented by letters: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
- Science Fiction: The 23 enigma plays a prominent role in the plot of The Illuminatus! Trilogy by Robert Shea and Robert Anton Wilson.
- Alphabetic writing: There are 26 letters in the Latin-derived English alphabet
- Science Fiction: The number 42, in the novel The Hitchhiker's Guide to the Galaxy by Douglas Adams, is the Answer to the Ultimate Question of Life, the Universe, and Everything which is calculated by an enormous supercomputer over a period of 7.5 million years.
- Phonology: 47 phonemes in English phonology in Received Pronunciation
102[edit]
(100; hundred)
ISO: hecto- (h)
- Demography: The population of Nassau Island, part of the Cook Islands, is around 100.
- European history: Groupings of 100 homesteads was a common administrative unit in Northern Europe and Great Britain (see Hundred (county subdivision)).
- Computing: There are 128 characters in the ASCII character set.
- Phonology: The Taa language is estimated to have between 130 and 164 distinct phonemes.
- Political Science: There were 193 member states of the United Nations as of 2011.
- Demography: Vatican City, the least populous country, has an approximate population of 842, as of July 2014.
103[edit]
(1000; thousand)
ISO: kilo- (k)
- Demography: The population of Ascension Island is 1,122.
- Typesetting: 2,000–3,000 letters on a typical typed page of text.
- Mathematics: 2,520 is the least common multiple of every integer under 10.
- Military history: 4,200 (Republic) or 5,200 (Empire) was the standard size of a Roman legion
- BioMed: the DNA of the simplest viruses has some 5,000 base pairs.
- Linguistics: Estimates for the linguistic diversity of living human languages or dialects range between 5,000 and 10,000 (SIL Ethnologue in 2009 listed 6,909 known living languages).
- Lexicography: 8,674 unique words in the Hebrew Bible
104[edit]
- BioMed: Each neuron in the human brain is estimated to connect to 10,000 others
- Demography: The population of Tuvalu was 10,544 in 2007.
- Lexicography: 14,500 unique English words occur in the King James Version of the Bible
- Language: There are 20,000–40,000 distinct Chinese characters.
- Grammar: Each regular verb in Cherokee can have 21,262 inflected forms.
- BioMed: Each human being is estimated to have 30,000 to 40,000 genes
- Mathematics: 65,537 is the largest known Fermat prime
- Memory: As of 2006, the largest number of decimal places of π that have been recited from memory is 67,890
105[edit]
- Demography: The population of Saint Vincent and the Grenadines was 100,982 in 2009.
- BioMed – Strands of hair on a head: The average human head has about 100,000–150,000 strands of hair
- Literature: approximately 100,000 verses (shlokas) in the Mahabharata
- Mathematics: 225,000 – The approximate number of entries in The On-Line Encyclopedia of Integer Sequences as of July 2013[5]
- Language: 267,000 words in James Joyce's Ulysses
- Genocide: 300,000 people killed in the Rape of Nanking
- Language – English words: The New Oxford Dictionary of English contains about 360,000 definitions for English words
- Literature: 564,000 words in War and Peace by Leo Tolstoy
- Literature: 930,000 words in the King James Version of the Bible
106[edit]
ISO: mega- (M)
- Demography: The population of Riga, Latvia was 1,003,949 in 2004, according to Eurostat.
- BioMed – Species: The World Resources Institute claims that approximately 1.4 million species have been named, out of an unknown number of total species (estimates range between 2 and 100 million species) Some scientists give 8.8 million species as an exact figure.
- Genocide: Approximately 800,000–1,500,000 (1.5 Million) Armenians were killed in the Armenian Genocide.
- Info: The freedb database of CD track listings has around 1,750,000 entries as of June 2005
- Mathematics – Playing cards: There are 2,598,960 different 5-card poker hands that can be dealt from a standard 52-card deck.
- Info – Web sites: As of March 11, 2016, Wikipedia contains approximately 5101000 articles in the English language
- Geography/Computing – Geographic places: The NIMA GEOnet Names Server contains approximately 3.88 million named geographic features outside the United States, with 5.34 million names. The USGS Geographic Names Information System claims to have almost 2 million physical and cultural geographic features within the United States.
- Genocide: Approximately 5,100,000–6,200,000 Jews were killed in the Holocaust.
107[edit]
- Demography: The population of Haiti was 10,085,214 in 2010.
- Mathematics: 12,988,816 is the number of domino tilings of an 8×8 checkerboard.
- Computing: 16,777,216 different colors can be generated using the hex code system in HTML (It has been estimated that the trichromatic color vision of the human eye can only distinguish about 1,000,000 different colors.).
- Science Fiction: In Isaac Asimov's Galactic Empire, in what we call 22,500 CE there are 25,000,000 different inhabited planets in the Galactic Empire, all inhabited by humansin Asimov's "human galaxy" scenario.
108[edit]
- Demography: The population of the Indian state of Bihar was 103,804,637 in 2007.
- Info – Books: The British Library claims that it holds over 150 million items. The Library of Congress claims that it holds approximately 148 million items. See The Gutenberg Galaxy
- Info – Web sites: As of November 2011, the Netcraft web survey estimates that there are 525,998,433 (526 million) distinct websites.
- Mathematics: More than 215,000,000 mathematical constants are collected on the Plouffe's Inverter as of 2010[6]
- Mathematics: 275,305,224 is the number of 5×5 normal magic squares, not counting rotations and reflections. This result was found in 1973 by Richard Schroeppel.
- Mathematics: 358,833,097 stellations of the rhombic triacontahedron
- Astronomy – Cataloged stars: The Guide Star Catalog II has entries on 998,402,801 distinct astronomical objects
109[edit]
ISO: giga- (G)
- Demography: The population of Africa reached 1,000,000,000 sometime in 2009.
- Demographics – India: 1,210,000,000 – approximate population of India in 2011
- Demographics – China: 1,347,000,000 – approximate population of the People's Republic of China in 2011.
- Internet: Approximately 1,500,000,000 active users were on Facebook as of October 2015.[7]
- Computing – Computational limit of a 32-bit CPU: 2 147 483 647 is equal to 231−1, and as such is the largest number which can fit into a signed (two's complement) 32-bit integer on a computer.
- BioMed – base pairs in the genome: approximately 3×109 base pairs in the human genome
- Linguistics: 3,400,000,000 – the total number of speakers of Indo-European languages, of which 2,400,000,000 are native speakers; the other 1,000,000,000 speak Indo-European languages as a second language
- Mathematics and computing: 4,294,967,295 (232 - 1), the product of the five known Fermat primes and the maximum value for a 32-bit unsigned integer in computing
- Computing – IPv4: 4,294,967,296 (232) possible unique IP addresses.
- Computing: 4,294,967,296 – the number of bytes in 4 gibibytes; in computation, the 32-bit computers can directly access 232 pieces of address space, this leads directly to the 4 gigabyte limit on main memory.
- Mathematics: 4,294,967,297 is a Fermat number and semiprime. It is the smallest number of the form
 which is not a prime number.
which is not a prime number. - Demographics – world population: 7,000,000,000 – Estimated population for the world on 31 October 2011, the Day of Seven Billion.
1010[edit]
- BioMed – bacteria in the human body: There are roughly 1010 bacteria in the human mouth[8]
- Computing – web pages: approximately 5.6×1010 web pages indexed by Google as of 2010.
1011[edit]
(100000000000; short scale: one hundred billion; long scale: hundred thousand million, or hundred milliard)
- BioMed – Neurons in the brain: approximately (1±0.2) × 1011 neurons in the human brain.[9]
- Paleodemography: approximately (1.2±0.3) × 1011 individuals of Homo sapiens have lived since speciation.[10]
- Astronomy – stars in our galaxy: of the order of 1011 stars in the Milky Way galaxy.[11]
- Astronomy –galaxies in the observable universe: of the order of 1011 galaxies in the observable universe.[12]
1012[edit]
ISO: tera- (T)
- Astronomy: Andromeda Galaxy, which is part of the same Local Group as our galaxy, contains about 1012 stars.
- BioMed – Bacteria on the human body: The surface of the human body houses roughly 1012 bacteria.[8]
- Wikipedia: 1.9786782 * 1012 is a rough estimate of the total number of links on Wikipedia.
- Marine biology: 3,500,000,000,000 (3.5 × 1012) – estimated population of fish in the ocean.
- Mathematics: 7,625,597,484,987 – a number that often appears when dealing with powers of 3. It can be expressed as
 ,
,  ,
,  ,
,  and 33 or when using Knuth's up-arrow notation it can be expressed as
and 33 or when using Knuth's up-arrow notation it can be expressed as  and
and 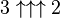 .
. - Mathematics: 1013 – The approximate number of known non-trivial zeros of the Riemann zeta function as of 2004.[13]
- Mathematics – Known digits of π: As of 2013, the number of known digits of π is 12,100,000,000,000 (1.21×1013).[14]
- BioMed – Cells in the human body: The human body consists of roughly 1014 cells, of which only 1013 are human.[15][16] The remaining 90% non-human cells (though much smaller and constituting much less mass) are bacteria, which mostly reside in the gastrointestinal tract, although the skin is also covered in bacteria.
- Computing – MAC-48: 281,474,976,710,656 (248) possible unique physical addresses.
- Mathematics: 953,467,954,114,363 is the largest known Motzkin prime.
1015[edit]
(1000000000000000; 10005; short scale: one quadrillion; long scale: one thousand billion, or one billiard)
ISO: peta- (P)
- BioMed – approximately 1015 synapses in the human brain [17]
- BioMed-Insects: 1,000,000,000,000,000 to 10,000,000,000,000,000 (1015 to 1016) – The estimated total number of ants on Earth alive at any one time (their biomass is approximately equal to the total biomass of the human race).[18]
- Computing: 9,007,199,254,740,992 (253) – number until which all integer values can exactly be represented in IEEE double precision floating-point format.
- Mathematics: 48,988,659,276,962,496 is the fifth taxicab number.
- Science Fiction: In Isaac Asimov's Galactic Empire, in what we call 22,500 CE there are 25,000,000 different inhabited planets in the Galactic Empire, all inhabited by humansin Asimov's "human galaxy" scenario, each with an average population of 2,000,000,000, thus yielding a total Galactic Empire population of approximately 50,000,000,000,000,000.
- Cryptography: There are 7.205759×1016 different possible keys in the obsolete 56 bit DES symmetric cipher.
1018[edit]
ISO: exa- (E)
- Computing – Manufacturing: An estimated 6×1018 transistors were produced worldwide in 2008.[19]
- Computing – Computational limit of a 64-bit CPU: 9,223,372,036,854,775,807 (about 9.22×1018) is equal to 263-1, and as such is the largest number which can fit into a signed (two's complement) 64-bit integer on a computer.
- Mathematics – NCAA Basketball Tournament: There are 9,223,372,036,854,775,808 (263) possible ways to enter the bracket.
- Mathematics – Bases: 9,439,829,801,208,141,318 (≈9.44×1018) is the 10th and largest number with more than one digit that can be written from base 2 to base 18 using only the digits 0 to 9.[20]
- BioMed – Insects: It has been estimated that the insect population of the Earth is about 1019.[21]
- Mathematics – Answer to the wheat and chessboard problem: When doubling the grains of wheat on each successive square of a chessboard, beginning with one grain of wheat on the first square, the final number of grains of wheat on all 64 squares of the chessboard when added up is 264−1 = 18,446,744,073,709,551,615 (≈1.84×1019).
- Mathematics – Legends: In the legend called the Tower of Brahma about a Hindu temple which contains a large room with three posts on one of which is 64 golden discs, the object of the mathematical game is for the Brahmins in the temple to move all of the discs to another pole so that they are in the same order, never placing a larger disc above a smaller disc. It would take 264−1 = 18,446,744,073,709,551,615 (≈1.84×1019) turns to complete the task (same number as the wheat and chessboard problem above).[22]
- Mathematics – Rubik's Cube: There are 43,252,003,274,489,856,000 (≈4.33×1019) different positions of a 3x3x3 Rubik's Cube
- Password strength: Usage of the 95-character set found on standard computer keyboards for a 10-character password yields a computationally intractable59,873,693,923,837,890,625 (9510, approximately 5.99×1019) permutations.
- Economics: Hyperinflation in Zimbabwe estimated in February 2009 by some economists at 10 sextillion percent,[23] or a factor of 1020
1021[edit]
(1000000000000000000000; 10007; short scale: one sextillion; long scale: one thousand trillion, or one trilliard)
ISO: zetta- (Z)
- Geo – Grains of sand: All the world's beaches combined have been estimated to hold roughly 1021 grains of sand.[24]
- Computing – Manufacturing: Intel predicted that there would be 1.2×1021 transistors in the world by 2015 [25] and Forbes estimated that 2.9×1021 transistors had been shipped up to 2014.[26]
- Mathematics – Sudoku: There are 6,670,903,752,021,072,936,960 (≈6.7×1021) 9×9 sudoku grids.[27]
- Astronomy – Stars: 70 sextillion = 7×1022, the estimated number of stars within range of telescopes (as of 2003).[28]
- Astronomy – Stars: in the range of 1023 to 1024 stars in the observable universe.[29]
- Mathematics: 146,361,946,186,458,562,560,000 (≈1.5×1023) is the fifth unitary perfect number.
- Chemistry – Physics: Avogadro constant (≈6×1023) is the number of constituents (e.g. atoms or molecules) in one mole of a substance, defined for convenience as expressing the order of magnitude separating the molecular from the macroscopic scale.
1024[edit]
ISO: yotta- (Y)
- Mathematics: 2,833,419,889,721,787,128,217,599 (≈2.8×1024) is a Woodall prime.
1027[edit]
(1000000000000000000000000000; 10009; short scale: one octillion; long scale: one thousand quadrillion, or one quadrilliard)
- BioMed – Atoms in the human body: the average human body contains roughly 7×1027 atoms[30]
- Mathematics – Poker: the number of unique combinations of hands and shared cards in a 10-player game of Texas Hold'em is approximately 2.117×1028, see Poker probability (Texas hold 'em).
1030[edit]
- BioMed – Bacterial cells on Earth: The number of bacterial cells on Earth is estimated at around 5,000,000,000,000,000,000,000,000,000,000, or 5 × 1030[31]
- Mathematics: The number of partitions of 1000 is 24,061,467,864,032,622,473,692,149,727,991.[32]
- Mathematics: 2108 = 324,518,553,658,426,726,783,156,020,576,256 is the largest known power of two not containing the digit '9' in its decimal representation.[33]
1033[edit]
(1000000000000000000000000000000000; 100011; short scale: one decillion; long scale: one thousand quintillion, or one quintilliard)
- Mathematics – Alexander's Star: There are 72,431,714,252,715,638,411,621,302,272,000,000 (about 7.24×1034) different positions of Alexander's Star
1036[edit]
(1000000000000000000000000000000000000; 100012; short scale: one undecillion; long scale: one sextillion)
- Physics: ke e2 / Gm2, the ratio of the electromagnetic to the gravitational forces between two protons, is roughly 1036.
- Mathematics:
 = 170,141,183,460,469,231,731,687,303,715,884,105,727 (≈1.7×1038) is a double Mersenne prime.
= 170,141,183,460,469,231,731,687,303,715,884,105,727 (≈1.7×1038) is a double Mersenne prime. - Computing: 2128 = 340,282,366,920,938,463,463,374,607,431,768,211,456 (≈3.40282367×1038), the theoretical maximum number of Internet addresses that can be allocated under the IPv6 addressing system, one more than the largest value that can be represented by a single-precision IEEE floating-point value, the total number of different Universally Unique Identifiers (UUIDs) that can be generated.
- Cryptography: 2128 = 340,282,366,920,938,463,463,374,607,431,768,211,456 (≈3.40282367×1038), the total number of different possible keys in the AES 128-bit key space(symmetric cipher).
1039[edit]
(1000000000000000000000000000000000000000; 100013; short scale: one duodecillion; long scale: one thousand sextillion, or one sextilliard)
- Cosmology: The Eddington–Dirac number is roughly 1040.
- Mathematics: 69,720,375,229,712,477,164,533,808,935,312,303,556,800 (≈6.97×1040) is the least common multiple of every integer from 1 to 100.
1042 to 10100[edit]
(1000000000000000000000000000000000000000000; 100014; short scale: one tredecillion; long scale: one septillion)
- Mathematics: 141×2141+1 = 393,050,634,124,102,232,869,567,034,555,427,371,542,904,833 (≈3.93×1044) is the second Cullen prime
- Mathematics: There are 7,401,196,841,564,901,869,874,093,974,498,574,336,000,000,000 (≈7.4×1045) possible permutations for the Rubik's Revenge (4x4x4 Rubik's Cube).
- Chess: 4.52×1046 is a proven upper bound for the number of legal chess positions.[34]
- Mathematics: 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 (≈8.08×1053) is the order of the Monster group.
- Cryptography: 2192 = 6,277,101,735,386,680,763,835,789,423,207,666,416,102,355,444,464,034,512,896 (6.27710174×1057), the total number of different possible keys in the AES 192-bit key space (symmetric cipher).
- Cosmology: 8×1060 is roughly the number of Planck time intervals since the universe is theorised to have been created in the Big Bang 13.799 ± 0.021 billion years ago.[35]
- Cosmology: 1×1063 is Archimedes’ estimate in The Sand Reckoner of the total number of grains of sand that could fit into the entire cosmos, the diameter of which he estimated in stadia to be what we call 2 light years.
- Mathematics – Cards: 52! = 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000 (≈8.07×1067) – the number of ways to order the cards in a 52-card deck.
- Mathematics: 1,808,422,353,177,349,564,546,512,035,512,530,001,279,481,259,854,248,860,454,348,989,451,026,887 (≈1.81×1072) – The largest known prime factorfound by ECM factorization as of 2010.[36]
- Mathematics: There are 282 870 942 277 741 856 536 180 333 107 150 328 293 127 731 985 672 134 721 536 000 000 000 000 000 (≈2.83×1074) possible permutations for the Professor's Cube (5x5x5 Rubik's Cube).
- Cryptography: 2256 = 115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665,640,564,039,457,584,007,913,129,639,936 (1.15792089×1077), the total number of different possible keys in the AES 256-bit key space (symmetric cipher).
- Cosmology: Various sources estimate the total number of fundamental particles in the observable universe to be within the range of 1080 to 1085.[37][38] However, these estimates are generally regarded as guesswork. (Compare the Eddington number, the estimated total number of protons in the observable universe.)
- Computing: 9.999 999×1096 is equal to the largest value that can be represented in the IEEE decimal32 floating-point format.
- Mathematics: 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000; 10100, agoogol
10100 (one googol) to 1010100 (one googolplex)[edit]
- Mathematics: There are 157 152 858 401 024 063 281 013 959 519 483 771 508 510 790 313 968 742 344 694 684 829 502 629 887 168 573 442 107 637 760 000 000 000 000 000 000 000 000 (≈1.57×10116) distinguishable permutations of the V-Cube 6 (6x6x6 Rubik's Cube).
- Chess: Shannon number, 10120, an estimation of the game-tree complexity of chess.
- Physics: 10120, the orders of magnitude of the vacuum catastrophe, the observed values of the quantum vacuum versus the values calculated by Quantum Field Theory.
- Physics: 8×10120, ratio of the mass-energy in the observable universe to the energy of a photon with a wavelength the size of the observable universe.
- History – Religion: Asaṃkhyeya is a Buddhist name for the number 10140. It is listed in the Avatamsaka Sutra and metaphorically means "innumerable" in the Sanskritlanguage of ancient India.
- Xiangqi: 10150, an estimation of the game-tree complexity of xiangqi.
- Mathematics: There are 19 500 551 183 731 307 835 329 126 754 019 748 794 904 992 692 043 434 567 152 132 912 323 232 706 135 469 180 065 278 712 755 853 360 682 328 551 719 137 311 299 993 600 000 000 000 000 000 000 000 000 000 000 000 (≈1.95 ×10160) distinguishable permutations of the V-Cube 7 (7x7x7 Rubik's Cube).
- Board games: 3.457×10181, number of ways to arrange the tiles in English Scrabble on a standard 15-by-15 Scrabble board.
- Physics: 4×10185, approximate number of Planck volumes in the observable universe.
- Physics: 6.84×10245, approximate number of Planck units that have ever existed in the observable universe.[39]
- Computing: 1.797 693 134 862 315 7×10308 is approximately equal to the largest value that can be represented in the IEEE double precision floating-point format.
- Go: 10365, an estimation of the game-tree complexity in the game of Go.[citation needed]
- Computing: (10 – 10−15)×10384 is equal to the largest value that can be represented in the IEEE decimal64 floating-point format.
- Mathematics: There are 66.909 260 871×101083) distinguishable permutations of the world's largest Rubik's cube (17x17x17).
- Computing: 1.189 731 495 357 231 765 05×104932 is approximately equal to the largest value that can be represented in the IEEE 80-bit x86 extended precision floating-point format.
- Computing: 1.189 731 495 357 231 765 085 759 326 628 007 0×104932 is approximately equal to the largest value that can be represented in the IEEE quadruple precision floating-point format.
- Computing: (10 – 10−33)×106144 is equal to the largest value that can be represented in the IEEE decimal128 floating-point format.
- Computing: 1010,000 − 1 is equal to the largest value that can be represented in Windows Phone's calculator.
- Mathematics: 26384405 + 44052638 is a 15,071-digit Leyland prime; the largest which has been proven as of 2010.[40]
- Mathematics: 3,756,801,695,685 × 2666,669 ± 1 are 200,700-digit twin primes; the largest known as of December 2011.[41]
- Mathematics: 18,543,637,900,515 × 2666,667 − 1 is a 200,701-digit Sophie Germain prime; the largest known as of April 2012.[42]
- Mathematics: approximately 7.76 · 10206,544 cattle in the smallest herd which satisfies the conditions of the Archimedes' cattle problem.
- Mathematics: 10290,253 - 2 × 10145,126 + 1 is a 290,253-digit palindromic prime, the largest known as of April 2012.[43]
- Mathematics: 1,098,133# – 1 is a 476,311-digit primorial prime; the largest known as of March 2012.[44]
- Mathematics: 150,209! + 1 is a 712,355-digit factorial prime; the largest known as of August 2011.[45]
- Mathematics – Literature: Jorge Luis Borges' Library of Babel contains at least
 books (this is a lower bound).[46]
books (this is a lower bound).[46] - Mathematics: 475,856524,288 + 1 is a 2,976,633-digit Generalized Fermat prime, the largest known as of December 2012.[47]
- Mathematics: 19,249 × 213,018,586 + 1 is a 3,918,990-digit Proth prime, the largest known Proth prime[48] and non-Mersenne prime as of 2010.[49]
- Mathematics: 274,207,281 − 1 is a 22,338,618-digit Mersenne prime; the largest known prime of any kind as of 2016.[49]
- Mathematics: 274,207,280 × (274,207,281 − 1) is a 44,677,235-digit perfect number, the largest known as of 2016.[50]
- Mathematics – History: 1080,000,000,000,000,000, largest named number in Archimedes' Sand Reckoner.
- Mathematics: 10googol (
 ), a googolplex.
), a googolplex.
Larger than 1010100 (one googolplex)[edit]
- Mathematics–Literature: The number of different ways in which the books in Luis Borges' Library of Babel can be arranged is
 , the factorial of the number of books in the Library of Babel.
, the factorial of the number of books in the Library of Babel. - Cosmology: In chaotic inflation theory, proposed by physicist Andrei Linde, our universe is one of many other universes with different physical constants that originated as part of our local section of the multiverse, owing to a vacuum that had not decayed to its ground state. According to Linde and Vanchurin, the total number of these universes is about
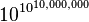 .[51]
.[51] - Mathematics:
 , order of magnitude of an upper bound that occurred in a proof of Skewes (this was later estimated to be closer to 1.397 × 10316).
, order of magnitude of an upper bound that occurred in a proof of Skewes (this was later estimated to be closer to 1.397 × 10316). - Mathematics:
 , order of magnitude of another upper bound in a proof of Skewes.
, order of magnitude of another upper bound in a proof of Skewes. - Mathematics: Moser's number "2 in a mega-gon" is approximately equal to 10↑↑↑...↑↑↑10, where there are 10↑↑257 arrows, the last two digits are ...56.
- Mathematics: Graham's number, the last ten digits of which are ...24641 95387. Arises as an upper bound solution to a problem in Ramsey theory. Representation in powers of 10 would be impractical (the number of digits in the exponent far exceeds the number of particles in the observable universe).
- Mathematics: TREE(3): appears in relation to a theorem on trees in graph theory. Representation of the number is difficult, but one weak lower bound is AA(187196)(1), where A(n) is a version of the Ackermann function.
- Mathematics: SSCG(3): appears in relation to the Robertson–Seymour theorem. Known to be greater than both TREE(3) and TREE(TREE(…TREE(3)…)) (the TREE function nested TREE(3) times with TREE(3) at the bottom).












No comments:
Post a Comment