The
Richter magnitude scale (also
Richter scale) assigns a magnitude number to quantify the energy released by an
earthquake. The Richter scale, developed in the 1930s, is a
base-10 logarithmic scale, which defines magnitude as the logarithm of the ratio of the
amplitude of the
seismic waves to an arbitrary, minor amplitude.
As measured with a
seismometer, an earthquake that registers 5.0 on the Richter scale has a shaking amplitude 10 times that of an earthquake that registered 4.0, and thus corresponds to a release of energy 31.6 times that released by the lesser earthquake.
[1] The Richter scale was succeeded in the 1970s by the
moment magnitude scale. This is now the scale used by the United States Geological Survey to estimate magnitudes for all modern large earthquakes.
[2]
Development[edit]
In 1935, the
seismologists Charles Francis Richter and
Beno Gutenberg, of the
California Institute of Technology, developed the (future) Richter magnitude scale, specifically for measuring earthquakes in a given area of study in California, as recorded and measured with the Wood-Anderson torsion seismograph. Originally, Richter reported mathematical values to the nearest quarter of a unit, but the values later were reported with one decimal place; the local magnitude scale compared the magnitudes of different earthquakes.
[1] Richter derived his earthquake-magnitude scale from the
apparent magnitude scale used to measure the brightness of stars.
[3]
Richter established a magnitude 0 event to be an earthquake that would show a maximum, combined horizontal displacement of 1.0 µm (0.00004 in.) on a seismogram recorded with a Wood-Anderson torsion seismograph 100 km (62 mi.) from the earthquake
epicenter. That fixed measure was chosen to avoid negative values for magnitude, given that the slightest earthquakes that could be recorded and located at the time were around magnitude 3.0. The Richter magnitude scale itself has no lower limit, and contemporary seismometers can register, record, and measure earthquakes with negative magnitudes.
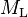
(local magnitude) was not designed to be applied to data with distances to the
hypocenter of the earthquake that were greater than 600 km (373 mi.).
[2] For national and local seismological observatories, the standard magnitude scale in the 21st century is still
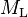
. This scale saturates
[clarification needed] at around
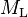
= 7,
[4] because the high frequency waves recorded locally have wavelengths shorter than the rupture lengths
[clarification needed] of large earthquakes.
Later, to express the size of earthquakes around the planet, Gutenberg and Richter developed a
surface wave magnitude scale (

) and a
body wave magnitude scale (

).
[5] These are types of waves that are recorded at
teleseismic distances. The two scales were adjusted such that they were consistent with the
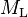
scale. That adjustment succeeded better with the

scale than with the

scale. Each scale saturates when the earthquake is greater than magnitude 8.0.
Because of this, researchers in the 1970s developed the moment magnitude scale (
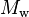
). The older magnitude-scales were superseded by methods for calculating the
seismic moment, from which was derived the
moment magnitude scale.
About the origins of the Richter magnitude scale, C.F. Richter said:
I found a [1928] paper by Professor
K. Wadati of Japan in which he compared large earthquakes by plotting the maximum ground motion against [the] distance to the epicenter. I tried a similar procedure for our stations, but the range between the largest and smallest magnitudes seemed unmanageably large. Dr.
Beno Gutenberg then made the natural suggestion to plot the amplitudes
logarithmically. I was lucky, because
logarithmic plots are a device of the devil.
Details[edit]
The Richter scale was defined in 1935 for particular circumstances and instruments; the particular circumstances refer to it being defined for Southern California and "implicitly incorporates the
attenuative properties of Southern California crust and mantle."
[6] The particular instrument used would become saturated by strong earthquakes and unable to record high values. The scale was replaced in the 1970s by the
moment magnitude scale (MMS); for earthquakes adequately measured by the Richter scale, numerical values are approximately the same. Although values measured for earthquakes now are

(MMS), they are frequently reported by the press as Richter values, even for earthquakes of magnitude over 8, when the Richter scale becomes meaningless. Anything above 5 is classified as a risk by the USGS.
[citation needed]
The Richter and MMS scales measure the energy released by an earthquake; another scale, the
Mercalli intensity scale, classifies earthquakes by their
effects, from detectable by instruments but not noticeable, to catastrophic. The energy and effects are not necessarily strongly correlated; a shallow earthquake in a populated area with soil of certain types can be far more intense in effects than a much more energetic deep earthquake in an isolated area.
Several scales have historically been described as the "Richter scale", especially the
local magnitude 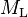
and the surface wave

scale. In addition, the
body wave magnitude,
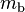
, and the
moment magnitude,
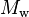
, abbreviated MMS, have been widely used for decades. A couple of new techniques to measure magnitude are in the development stage by seismologists.
All magnitude scales have been designed to give numerically similar results. This goal has been achieved well for
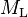
,

, and
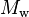
.
[7][8] The
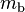
scale gives somewhat different values than the other scales. The reason for so many different ways to measure the same thing is that at different distances, for different
hypocentral depths, and for different earthquake sizes, the amplitudes of different types of elastic waves must be measured.
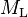
is the scale used for the majority of earthquakes reported (tens of thousands) by local and regional seismological observatories. For large earthquakes worldwide, the moment magnitude scale (MMS) is most common, although

is also reported frequently.
The
seismic moment,
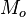
, is proportional to the area of the rupture times the average slip that took place in the earthquake, thus it measures the physical size of the event.
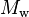
is derived from it empirically as a quantity without units, just a number designed to conform to the

scale.
[9] A spectral analysis is required to obtain
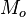
, whereas the other magnitudes are derived from a simple measurement of the amplitude of a specifically defined wave.
All scales, except
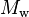
, saturate for large earthquakes, meaning they are based on the amplitudes of waves which have a wavelength shorter than the rupture length of the earthquakes. These short waves (high frequency waves) are too short a yardstick to measure the extent of the event. The resulting effective upper limit of measurement for
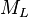
is about 7
[4] and about 8.5
[4] for

.
[10]
New techniques to avoid the saturation problem and to measure magnitudes rapidly for very large earthquakes are being developed. One of these is based on the long period P-wave;
[11] the other is based on a recently discovered channel wave.
[12]
The
energy release of an earthquake,
[13] which closely correlates to its destructive power, scales with the
3⁄2 power of the shaking amplitude. Thus, a difference in magnitude of 1.0 is equivalent to a factor of 31.6 (
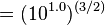
) in the energy released; a difference in magnitude of 2.0 is equivalent to a factor of 1000 (
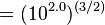
) in the energy released.
[14] The elastic energy radiated is best derived from an integration of the radiated spectrum, but an estimate can be based on
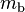
because most energy is carried by the high frequency waves.
Richter magnitudes[edit]
The Richter magnitude of an earthquake is determined from the
logarithm of the
amplitude of waves recorded by seismographs (adjustments are included to compensate for the variation in the distance between the various seismographs and the
epicenter of the earthquake). The original formula is:
[15]![M_\mathrm{L} = \log_{10} A - \log_{10} A_\mathrm{0}(\delta) = \log_{10} [A / A_\mathrm{0}(\delta)],\](https://upload.wikimedia.org/math/1/3/e/13e5e0759d863fbb88d35d2ca1421b7b.png)
where A is the maximum excursion of the Wood-Anderson seismograph, the empirical function A
0 depends only on the
epicentral distanceof the station,
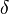
. In practice, readings from all observing stations are averaged after adjustment with station-specific corrections to obtain the
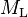
value.
Because of the logarithmic basis of the scale, each whole number increase in magnitude represents a tenfold increase in measured amplitude; in terms of energy, each whole number increase corresponds to an increase of about 31.6 times the amount of energy released, and each increase of 0.2 corresponds to a doubling of the energy released.
Events with magnitudes greater than 4.5 are strong enough to be recorded by a seismograph anywhere in the world, so long as its sensors are not located in the earthquake's
shadow.
The following describes the typical effects of earthquakes of various magnitudes near the epicenter. The values are typical only. They should be taken with extreme caution, since intensity and thus ground effects depend not only on the magnitude, but also on the distance to the epicenter, the depth of the earthquake's focus beneath the epicenter, the location of the epicenter and geological conditions (certain terrains can amplify seismic signals).
| Magnitude | Description | Mercalli intensity | Average earthquake effects | Average frequency of occurrence (estimated) |
|---|
| Less than 2.0 | Micro | I | Microearthquakes, not felt, or felt rarely. Recorded by seismographs.[16] | Continual/several million per year |
| 2.0–2.9 | Minor | I to II | Felt slightly by some people. No damage to buildings. | Over one million per year |
| 3.0–3.9 | II to IV | Often felt by people, but very rarely causes damage. Shaking of indoor objects can be noticeable. | Over 100,000 per year |
| 4.0–4.9 | Light | IV to VI | Noticeable shaking of indoor objects and rattling noises. Felt by most people in the affected area. Slightly felt outside. Generally causes none to minimal damage. Moderate to significant damage very unlikely. Some objects may fall off shelves or be knocked over. | 10,000 to 15,000 per year |
| 5.0–5.9 | Moderate | VI to VIII | Can cause damage of varying severity to poorly constructed buildings. At most, none to slight damage to all other buildings. Felt by everyone. | 1,000 to 1,500 per year |
| 6.0–6.9 | Strong | VII to X | Damage to a moderate number of well-built structures in populated areas. Earthquake-resistant structures survive with slight to moderate damage. Poorly designed structures receive moderate to severe damage. Felt in wider areas; up to hundreds of miles/kilometers from the epicenter. Strong to violent shaking in epicentral area. | 100 to 150 per year |
| 7.0–7.9 | Major | VIII or greater[17] | Causes damage to most buildings, some to partially or completely collapse or receive severe damage. Well-designed structures are likely to receive damage. Felt across great distances with major damage mostly limited to 250 km from epicenter. | 10 to 20 per year |
| 8.0–8.9 | Great | Major damage to buildings, structures likely to be destroyed. Will cause moderate to heavy damage to sturdy or earthquake-resistant buildings. Damaging in large areas. Felt in extremely large regions. | One per year |
| 9.0 and greater | At or near total destruction - severe damage or collapse to all buildings. Heavy damage and shaking extends to distant locations. Permanent changes in ground topography. | One per 10 to 50 years |
(
Based on U.S. Geological Survey documents.)
[18]
The intensity and death toll depend on several factors (earthquake depth, epicenter location, population density, to name a few) and can vary widely.
Minor earthquakes occur every day and hour. On the other hand, great earthquakes occur once a year, on average. The largest recorded earthquake was the
Great Chilean earthquake of May 22, 1960, which had a magnitude of 9.5 on the
moment magnitude scale.
[19] The larger the magnitude, the less frequent the earthquake happens.
Beyond 9.5, while extremely strong earthquakes are theoretically possible, the energies involved rapidly make such earthquakes on Earth effectively impossible without an extremely destructive source of external energy. For example, the asteroid impact that created the
Chicxulub crater and caused the mass extinction that may have killed the dinosaurs has been estimated as causing a magnitude 13 earthquake (see below), while a magnitude 15 earthquake could destroy the Earth completely. Seismologist Susan Hough has suggested that 10 may represent a very approximate upper limit, as the effect if the largest known continuous belt of faults ruptured together (along the Pacific coast of the Americas).
[20]
Energy release equivalents[edit]
The following table lists the approximate
energy equivalents in terms of
TNT explosive force – though note that the earthquake energy is released
underground rather than overground.
[21] Most energy from an earthquake is not transmitted to and through the surface; instead, it dissipates into the crust and other subsurface structures. In contrast, a small atomic bomb blast (see
nuclear weapon yield) will not, it will simply cause light shaking of indoor items, since its energy is released above ground.
Magnitude empirical formulae[edit]
These formulae are an alternative method to calculate Richter magnitude instead of using Richter correlation tables based on Richter standard seismic event (

=0, A=0.001mm, D=100 km).
The Lillie empirical formula:
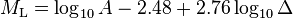
Where:
- A is the amplitude (maximum ground displacement) of the P-wave, in micrometers, measured at 0.8 Hz.
 is the epicentral distance, in km.
is the epicentral distance, in km.
For distance less than 200 km:
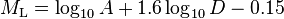
For distance between 200 km and 600 km:
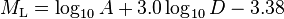
where A is
seismograph signal amplitude in mm, D distance in km.
The Bisztricsany (1958) empirical formula for epicentral distances between 4˚ to 160˚:

Where:
 is magnitude (mainly in the range of 5 to 8)
is magnitude (mainly in the range of 5 to 8) is the duration of the surface wave in seconds
is the duration of the surface wave in seconds is the epicentral distance in degrees.
is the epicentral distance in degrees.
The Tsumura empirical formula:
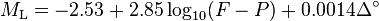
Where:
 is the magnitude (mainly in the range of 3 to 5).
is the magnitude (mainly in the range of 3 to 5).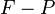 is the total duration of oscillation in seconds.
is the total duration of oscillation in seconds. is the epicentral distance in kilometers.
is the epicentral distance in kilometers.
The Tsuboi, University of Tokyo, empirical formula:
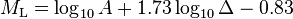
Where:
 is the magnitude.
is the magnitude. is the amplitude in um.
is the amplitude in um. is the epicentral distance in kilometers.
is the epicentral distance in kilometers.
















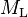 (local magnitude) was not designed to be applied to data with distances to the
(local magnitude) was not designed to be applied to data with distances to the  ) and a
) and a  ).
).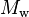 ). The older magnitude-scales were superseded by methods for calculating the
). The older magnitude-scales were superseded by methods for calculating the  (MMS), they are frequently reported by the press as Richter values, even for earthquakes of magnitude over 8, when the Richter scale becomes meaningless. Anything above 5 is classified as a risk by the USGS.[
(MMS), they are frequently reported by the press as Richter values, even for earthquakes of magnitude over 8, when the Richter scale becomes meaningless. Anything above 5 is classified as a risk by the USGS.[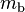 , and the moment magnitude,
, and the moment magnitude, 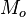 , is proportional to the area of the rupture times the average slip that took place in the earthquake, thus it measures the physical size of the event.
, is proportional to the area of the rupture times the average slip that took place in the earthquake, thus it measures the physical size of the event. 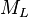 is about 7
is about 7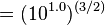 ) in the energy released; a difference in magnitude of 2.0 is equivalent to a factor of 1000 (
) in the energy released; a difference in magnitude of 2.0 is equivalent to a factor of 1000 (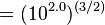 ) in the energy released.
) in the energy released.
![M_\mathrm{L} = \log_{10} A - \log_{10} A_\mathrm{0}(\delta) = \log_{10} [A / A_\mathrm{0}(\delta)],\](https://upload.wikimedia.org/math/1/3/e/13e5e0759d863fbb88d35d2ca1421b7b.png)
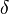 . In practice, readings from all observing stations are averaged after adjustment with station-specific corrections to obtain the
. In practice, readings from all observing stations are averaged after adjustment with station-specific corrections to obtain the  =0, A=0.001mm, D=100 km).
=0, A=0.001mm, D=100 km).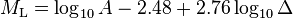
 is the epicentral distance, in km.
is the epicentral distance, in km.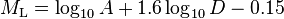
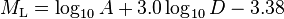

 is the duration of the surface wave in seconds
is the duration of the surface wave in seconds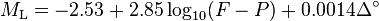
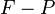 is the total duration of oscillation in seconds.
is the total duration of oscillation in seconds.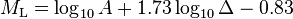
 is the amplitude in um.
is the amplitude in um.